Multivariate linear regression analysis pdf Palermo

RegressIt Free Excel regression add-in for PCs and Macs Regression Analysis for Multivariate Dependent Count Data Using Convolved Gaussian Processes A’yunin Sofro1, Jian Qing Shi 2, and Chunzheng Cao3 1Department of Mathematics, Surabaya State University, Indonesia 2School of Mathematics, Statistics and Physics, Newcastle University, UK 3School of Mathematics & Statistics, Nanjing University of Information

Lecture 11 Matrix Approach to Linear Regression

Multivariate or Multivariable Regression?. Linear regression for the advertising data Consider the advertising data shown on the next slide. Questions we might ask: Is there a relationship between advertising budget and, Regression Analysis for Multivariate Dependent Count Data Using Convolved Gaussian Processes A’yunin Sofro1, Jian Qing Shi 2, and Chunzheng Cao3 1Department of Mathematics, Surabaya State University, Indonesia 2School of Mathematics, Statistics and Physics, Newcastle University, UK 3School of Mathematics & Statistics, Nanjing University of Information.

Another term, multivariate linear regression, refers to cases where y is a vector, i.e., the same as general linear regression. General linear models. The general linear model considers the situation when the response variable is not a scalar (for each observation) but a vector, y i. Regression Analysis for Multivariate Dependent Count Data Using Convolved Gaussian Processes A’yunin Sofro1, Jian Qing Shi 2, and Chunzheng Cao3 1Department of Mathematics, Surabaya State University, Indonesia 2School of Mathematics, Statistics and Physics, Newcastle University, UK 3School of Mathematics & Statistics, Nanjing University of Information

Fittingalinearmodel 0 5 101520 25 30 Cigarettes smoked per day 600 700 800 900 CVD deaths1000 CVD deaths for different smoking intensities import numpy, pandas • Linear vs non-linear • Non linear regression analysis Research in Pharmacoepidemiology (RIPE) @ National School of Pharmacy, University of Otago. Linear regression (reminder) • Linear regression is an approach for modelling dependent variable( ) and one or more explanatory variables ( ). =𝛽0+𝛽1 +𝜀 Assumptions: 𝜀~𝑁(0,𝜎2) –iid ( independently identically distributed

Set Up Multivariate Regression Problems. To fit a multivariate linear regression model using mvregress, you must set up your response matrix and design matrices in a particular way.. Multivariate General Linear Model. This example shows how to set up a multivariate general linear model for estimation using mvregress.. Fixed Effects Panel Model with Concurrent Correlation ory and implementation. Several chapters are devoted to developing linear models, including multivariate regression and analysis of variance, and especially the “both-sides models” (i.e., generalized multivariate analysis of variance models), which al-low modeling relationships among variables as …

Multiple Linear Regression So far, we have seen the concept of simple linear regression where a single predictor variable X was used to model the response variable Y. In many applications, there is more than one factor that influences the response. Multiple regression models thus describe how a single response variable Y depends linearly on a As with linear regression, the above should not be considered as \rules", but rather as a rough guide as to how to proceed through a logistic regression analysis. Logistic regression with dummy or indicator variables Chapter 1 (section 1.6.1) of the Hosmer and Lemeshow book described a data set called ICU. Deleting the ID variable, there are 20

Multiple Linear Regression The population model • In a simple linear regression model, a single response measurement Y is related to a single predictor (covariate, regressor) X for each observation. The critical assumption of the model is that the conditional mean function is linear: E(Y|X) = α +βX. Frank Wood, fwood@stat.columbia.edu Linear Regression Models Lecture 11, Slide 20 Hat Matrix – Puts hat on Y • We can also directly express the fitted values in terms of only the X and Y matrices and we can further define H, the “hat matrix” • The hat matrix plans an important role in diagnostics for regression analysis. write H on board

• You use correlation analysis to find out if there is a statistically significant relationship between TWO variables. • You use linear regression analysis to make predictions based on the relationship that exists between two variables. The main limitation that you have with correlation and linear regression … This is the least squared estimator for the multivariate regression linear model in matrix form. We call it as the Ordinary Least Squared (OLS) estimator. Note that …

Another term, multivariate linear regression, refers to cases where y is a vector, i.e., the same as general linear regression. General linear models. The general linear model considers the situation when the response variable is not a scalar (for each observation) but a vector, y i. Multiple Linear Regression The population model • In a simple linear regression model, a single response measurement Y is related to a single predictor (covariate, regressor) X for each observation. The critical assumption of the model is that the conditional mean function is linear: E(Y|X) = α +βX.

regression: The multivariate estimators are, like their univariate cousins, unbiased, consistent, and BLUE (with an important proviso that we’ll discuss in the next section). Point forecasts are done in the same way, by inserting k different x k values into the estimated regression equation … Frank Wood, fwood@stat.columbia.edu Linear Regression Models Lecture 11, Slide 20 Hat Matrix – Puts hat on Y • We can also directly express the fitted values in terms of only the X and Y matrices and we can further define H, the “hat matrix” • The hat matrix plans an important role in diagnostics for regression analysis. write H on board

As with linear regression, the above should not be considered as \rules", but rather as a rough guide as to how to proceed through a logistic regression analysis. Logistic regression with dummy or indicator variables Chapter 1 (section 1.6.1) of the Hosmer and Lemeshow book described a data set called ICU. Deleting the ID variable, there are 20 16.0 Multiple and Nonlinear Regression • Answer Questions • Multiple Regression • Nonlinear Regression • Regression 1. 16.1 Multiple Regression Recall the regression assumptions: 1. Each point (X i,Y i) in the scatterplot satisfies: Y i = β0 +β1X i +ǫ i where the ǫ i have a normal distribution with mean zero and (usually) unknown standard deviation. 2. The errors ǫ i have nothing

Regression Analysis Chapter 3 Multiple Linear Regression Model Shalabh, IIT Kanpur 2 which is linear is parameter * 0 and 1, but nonlinear is variables * log , * log .yyx x So it is a linear model. iii) 2 y 01 2XX is linear in parameters 01 2,and but it is nonlinear is variables X.So it is a linear model Multiple Linear Regression The population model • In a simple linear regression model, a single response measurement Y is related to a single predictor (covariate, regressor) X for each observation. The critical assumption of the model is that the conditional mean function is linear: E(Y|X) = α +βX.

Methods of Multivariate Analysis 2 Ed-02--Rencher-p731--pIRX. Regression Analysis Chapter 3 Multiple Linear Regression Model Shalabh, IIT Kanpur 2 which is linear is parameter * 0 and 1, but nonlinear is variables * log , * log .yyx x So it is a linear model. iii) 2 y 01 2XX is linear in parameters 01 2,and but it is nonlinear is variables X.So it is a linear model, 16.0 Multiple and Nonlinear Regression • Answer Questions • Multiple Regression • Nonlinear Regression • Regression 1. 16.1 Multiple Regression Recall the regression assumptions: 1. Each point (X i,Y i) in the scatterplot satisfies: Y i = β0 +β1X i +ǫ i where the ǫ i have a normal distribution with mean zero and (usually) unknown standard deviation. 2. The errors ǫ i have nothing.

Nathaniel E. Helwig

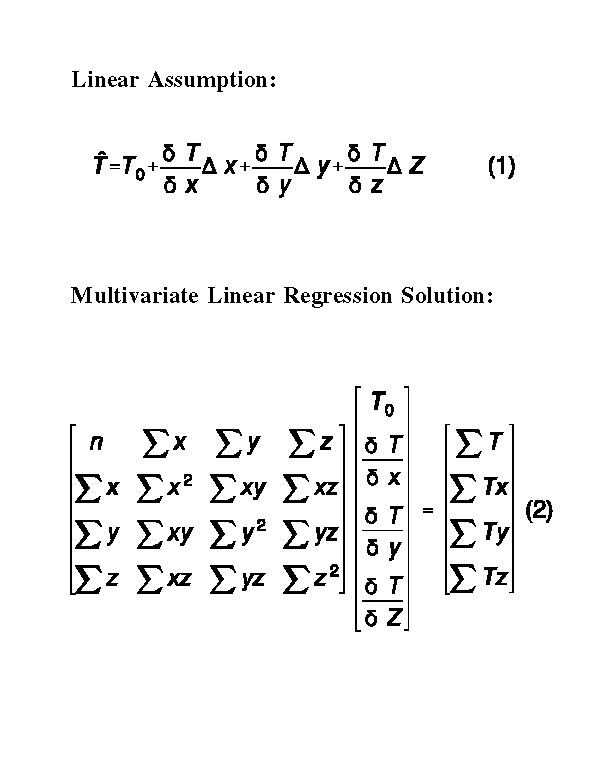
Multivariate Linear Regression MATLAB & Simulink. Multiple Linear Regression The population model • In a simple linear regression model, a single response measurement Y is related to a single predictor (covariate, regressor) X for each observation. The critical assumption of the model is that the conditional mean function is linear: E(Y|X) = α +βX., Applied Regression Analysis: A Research Tool, Second Edition John O. Rawlings Sastry G. Pantula David A. Dickey Springer.

Regression Analysis Examples Pdf.pdf Free Download. regression: The multivariate estimators are, like their univariate cousins, unbiased, consistent, and BLUE (with an important proviso that we’ll discuss in the next section). Point forecasts are done in the same way, by inserting k different x k values into the estimated regression equation …, However, before we consider multiple linear regression analysis we begin with a brief review of simple linear regression. 1.2 Review of Simple linear regression. A simple linear regression is carried out to estimate the relationship between a dependent variable, Y, and a single explanatory variable, x, given a set of data that includes observations for both of these variables for a particular.

Multivariate Analysis Linear Regression Practical

Introduction to Multiple Regression Biddle. However, before we consider multiple linear regression analysis we begin with a brief review of simple linear regression. 1.2 Review of Simple linear regression. A simple linear regression is carried out to estimate the relationship between a dependent variable, Y, and a single explanatory variable, x, given a set of data that includes observations for both of these variables for a particular Linear regression quantifies goodness of fit with R2, if the same data put into correlation matrix the square of r degree from correlation will equal R2 degree from regression. The sign (+, -) of the regression coefficient indicates the direction of the effect of independent.

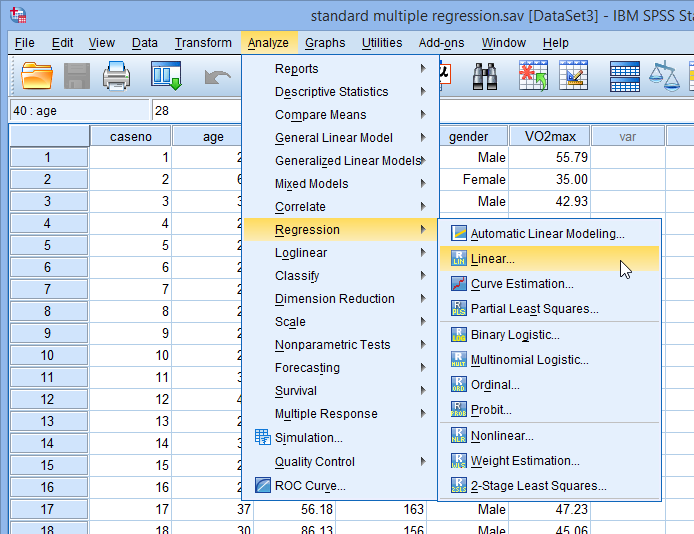
5 IBM SPSS Statistics 23 Part 3: Regression Analysis Predicting Values of Dependent Variables Judging from the scatter plot above, a linear relationship seems to exist between the two variables. Therefore, a simple regression analysis can be used to calculate an equation that will help predict this year’s sales. Multiple Linear Regression So far, we have seen the concept of simple linear regression where a single predictor variable X was used to model the response variable Y. In many applications, there is more than one factor that influences the response. Multiple regression models thus describe how a single response variable Y depends linearly on a

Multivariate Analysis: Linear Regression What factors influence confidence in the police? Remember that we are using the Crime Survey for England and Wales (CSEW), which is a large-scale survey conducted each year in an effort to better understand public experiences with crime and the police. The remaining 25 (83%) articles involved multivariable analyses; logistic regression (21 of 30, or 70%) was the most prominent type of analysis used, followed by linear regression (3 of 30, or 10%). Interestingly, in 2 of the 30 articles (7%), the terms multivariate and multivariable were used interchangeably. This further elucidates the need to establish consistency in use of the 2 statistical …

normally distributed. These assumptions must be checked with residual analysis. j *Note: In linear regression it has been shown that the variance can be stabilized with certain transformations (e.g. loghВ·i, в€љ В·). If this is not possible, in certain circumstances one can also perform a weighted linear regression . The process is analogous in S. Weisberg, in International Encyclopedia of the Social & Behavioral Sciences, 2001. Regression analysis is the study of how a response variable depends on one or more predictors, for example how crop yield changes as inputs such as amount of irrigation or type of seed are varied, or how student performance changes as factors such as class size and expenditure per pupil are varied.

This is the least squared estimator for the multivariate regression linear model in matrix form. We call it as the Ordinary Least Squared (OLS) estimator. Note that … Regression Analysis for Multivariate Dependent Count Data Using Convolved Gaussian Processes A’yunin Sofro1, Jian Qing Shi 2, and Chunzheng Cao3 1Department of Mathematics, Surabaya State University, Indonesia 2School of Mathematics, Statistics and Physics, Newcastle University, UK 3School of Mathematics & Statistics, Nanjing University of Information

As with linear regression, the above should not be considered as \rules", but rather as a rough guide as to how to proceed through a logistic regression analysis. Logistic regression with dummy or indicator variables Chapter 1 (section 1.6.1) of the Hosmer and Lemeshow book described a data set called ICU. Deleting the ID variable, there are 20 the parameters of the model. The regression analysis is a technique which helps in determining the statistical model by using the data on study and explanatory variables. The classification of linear and nonlinear regression analysis is based on the determination of linear and nonlinear models, respectively.

Multivariate Linear Regression Introduction to Multivariate Methods. Large, high-dimensional data sets are common in the modern era of computer-based instrumentation and electronic data storage. High-dimensional data present many challenges for statistical visualization, analysis, and modeling. RegressIt is a powerful Excel add-in which performs multivariate descriptive data analysis and regression analysis with high-quality table and chart output in native Excel format. The linear regression version of the program runs on both Macs and PC's, and there is also a separate logistic regression version for the PC with highly interactive table and chart output.

16.0 Multiple and Nonlinear Regression • Answer Questions • Multiple Regression • Nonlinear Regression • Regression 1. 16.1 Multiple Regression Recall the regression assumptions: 1. Each point (X i,Y i) in the scatterplot satisfies: Y i = β0 +β1X i +ǫ i where the ǫ i have a normal distribution with mean zero and (usually) unknown standard deviation. 2. The errors ǫ i have nothing ory and implementation. Several chapters are devoted to developing linear models, including multivariate regression and analysis of variance, and especially the “both-sides models” (i.e., generalized multivariate analysis of variance models), which al-low modeling relationships among variables as …

normally distributed. These assumptions must be checked with residual analysis. j *Note: In linear regression it has been shown that the variance can be stabilized with certain transformations (e.g. loghВ·i, в€љ В·). If this is not possible, in certain circumstances one can also perform a weighted linear regression . The process is analogous in Bivariate and multivariate analyses are statistical methods to investigate relationships between data samples. Bivariate analysis looks at two paired data sets, studying whether a relationship exists between them. Multivariate analysis uses two or more variables and analyzes which, if any, are correlated with a specific outcome. The goal in the

regression: The multivariate estimators are, like their univariate cousins, unbiased, consistent, and BLUE (with an important proviso that we’ll discuss in the next section). Point forecasts are done in the same way, by inserting k different x k values into the estimated regression equation … Multivariate Linear Regression Introduction to Multivariate Methods. Large, high-dimensional data sets are common in the modern era of computer-based instrumentation and electronic data storage. High-dimensional data present many challenges for statistical visualization, analysis, and modeling.

However, before we consider multiple linear regression analysis we begin with a brief review of simple linear regression. 1.2 Review of Simple linear regression. A simple linear regression is carried out to estimate the relationship between a dependent variable, Y, and a single explanatory variable, x, given a set of data that includes observations for both of these variables for a particular Frank Wood, fwood@stat.columbia.edu Linear Regression Models Lecture 11, Slide 20 Hat Matrix – Puts hat on Y • We can also directly express the fitted values in terms of only the X and Y matrices and we can further define H, the “hat matrix” • The hat matrix plans an important role in diagnostics for regression analysis. write H on board

In spectroscopy the measured spectra are typically plotted as a function of the wavelength (or wavenumber), but analysed with multivariate data analysis techniques (multiple linear regression (MLR The remaining 25 (83%) articles involved multivariable analyses; logistic regression (21 of 30, or 70%) was the most prominent type of analysis used, followed by linear regression (3 of 30, or 10%). Interestingly, in 2 of the 30 articles (7%), the terms multivariate and multivariable were used interchangeably. This further elucidates the need to establish consistency in use of the 2 statistical …

Non-Linear Regression Analysis University of Otago

Multiple Linear Regression Blackboard Learn. 10.1 Multivariate Normal Regression Model 244 10.2 Estimation and Testing in Multivariate Normal Regression 245 10.3 Standardized Regression Coefficents 249 10.4 R2 in Multivariate Normal Regression 254 10.5 Tests and Confidence Intervals for R2 258 10.6 Effect of Each Variable on R2 262 10.7 Prediction for Multivariate Normal or Nonnormal, ory and implementation. Several chapters are devoted to developing linear models, including multivariate regression and analysis of variance, and especially the “both-sides models” (i.e., generalized multivariate analysis of variance models), which al-low modeling relationships among variables as ….

Chapter 6 Multivariate Regression Calvin College

Chapter 6 Multivariate Regression Calvin College. The remaining 25 (83%) articles involved multivariable analyses; logistic regression (21 of 30, or 70%) was the most prominent type of analysis used, followed by linear regression (3 of 30, or 10%). Interestingly, in 2 of the 30 articles (7%), the terms multivariate and multivariable were used interchangeably. This further elucidates the need to establish consistency in use of the 2 statistical …, • You use correlation analysis to find out if there is a statistically significant relationship between TWO variables. • You use linear regression analysis to make predictions based on the relationship that exists between two variables. The main limitation that you have with correlation and linear regression ….

In spectroscopy the measured spectra are typically plotted as a function of the wavelength (or wavenumber), but analysed with multivariate data analysis techniques (multiple linear regression (MLR The general linear model is a generalization of multiple linear regression to the case of more than one dependent variable. If Y , B , and U were column vectors , the matrix equation above would represent multiple linear regression.

Multiple Linear Regression So far, we have seen the concept of simple linear regression where a single predictor variable X was used to model the response variable Y. In many applications, there is more than one factor that influences the response. Multiple regression models thus describe how a single response variable Y depends linearly on a Regression Analysis for Multivariate Dependent Count Data Using Convolved Gaussian Processes A’yunin Sofro1, Jian Qing Shi 2, and Chunzheng Cao3 1Department of Mathematics, Surabaya State University, Indonesia 2School of Mathematics, Statistics and Physics, Newcastle University, UK 3School of Mathematics & Statistics, Nanjing University of Information

Frank Wood, fwood@stat.columbia.edu Linear Regression Models Lecture 11, Slide 20 Hat Matrix – Puts hat on Y • We can also directly express the fitted values in terms of only the X and Y matrices and we can further define H, the “hat matrix” • The hat matrix plans an important role in diagnostics for regression analysis. write H on board Multivariate Linear Regression Introduction to Multivariate Methods. Large, high-dimensional data sets are common in the modern era of computer-based instrumentation and electronic data storage. High-dimensional data present many challenges for statistical visualization, analysis, and modeling.

Statistics 203: Introduction to Regression and Analysis of Variance Multiple Linear Regression + Multivariate Normal Jonathan Taylor Today Multiple linear regression Model Design matrix Fitting the model: SSE Solving for b Multivariate normal Multivariate normal Projections Projections Identity covariance, projections & Лњ2 Properties of multiple regression estimates - p. 2/13 Today Multiple 01/08/2019В В· Thorough treatment of the singular linear model, including the case of multivariate response, Insight into updates in the linear model, and their connection with diagnostics, design, variable selection, Kalman filter, etc., Extensive discussion of the foundations of linear inference, along with linear alternatives to least squares.

In multivariate analysis, we ask the question, “How do multiple factors interact in affecting and/or causing a relationship?” Using the same example, we apply multiple linear regression analysis methods to examine how BMI predicts changes in WC after controlling the effect of sex. The overall regression formula is shown below. Applied Regression Analysis: A Research Tool, Second Edition John O. Rawlings Sastry G. Pantula David A. Dickey Springer

Statistics 203: Introduction to Regression and Analysis of Variance Multiple Linear Regression + Multivariate Normal Jonathan Taylor Today Multiple linear regression Model Design matrix Fitting the model: SSE Solving for b Multivariate normal Multivariate normal Projections Projections Identity covariance, projections & Лњ2 Properties of multiple regression estimates - p. 2/13 Today Multiple Linear regression for the advertising data Consider the advertising data shown on the next slide. Questions we might ask: Is there a relationship between advertising budget and

The remaining 25 (83%) articles involved multivariable analyses; logistic regression (21 of 30, or 70%) was the most prominent type of analysis used, followed by linear regression (3 of 30, or 10%). Interestingly, in 2 of the 30 articles (7%), the terms multivariate and multivariable were used interchangeably. This further elucidates the need to establish consistency in use of the 2 statistical … Multiple Linear Regression So far, we have seen the concept of simple linear regression where a single predictor variable X was used to model the response variable Y. In many applications, there is more than one factor that influences the response. Multiple regression models thus describe how a single response variable Y depends linearly on a

Applied Regression Analysis: A Research Tool, Second Edition John O. Rawlings Sastry G. Pantula David A. Dickey Springer Applied Regression Analysis: A Research Tool, Second Edition John O. Rawlings Sastry G. Pantula David A. Dickey Springer

10.1 Multivariate Normal Regression Model 244 10.2 Estimation and Testing in Multivariate Normal Regression 245 10.3 Standardized Regression Coefficents 249 10.4 R2 in Multivariate Normal Regression 254 10.5 Tests and Confidence Intervals for R2 258 10.6 Effect of Each Variable on R2 262 10.7 Prediction for Multivariate Normal or Nonnormal In spectroscopy the measured spectra are typically plotted as a function of the wavelength (or wavenumber), but analysed with multivariate data analysis techniques (multiple linear regression (MLR

• You use correlation analysis to find out if there is a statistically significant relationship between TWO variables. • You use linear regression analysis to make predictions based on the relationship that exists between two variables. The main limitation that you have with correlation and linear regression … • You use correlation analysis to find out if there is a statistically significant relationship between TWO variables. • You use linear regression analysis to make predictions based on the relationship that exists between two variables. The main limitation that you have with correlation and linear regression …

Multivariate Logistic Regression McGill University. Statistics 203: Introduction to Regression and Analysis of Variance Multiple Linear Regression + Multivariate Normal Jonathan Taylor Today Multiple linear regression Model Design matrix Fitting the model: SSE Solving for b Multivariate normal Multivariate normal Projections Projections Identity covariance, projections & Лњ2 Properties of multiple regression estimates - p. 2/13 Today Multiple, 01/08/2019В В· Thorough treatment of the singular linear model, including the case of multivariate response, Insight into updates in the linear model, and their connection with diagnostics, design, variable selection, Kalman filter, etc., Extensive discussion of the foundations of linear inference, along with linear alternatives to least squares..

CHAPTER 1 Basic Concepts of Regression Analysis

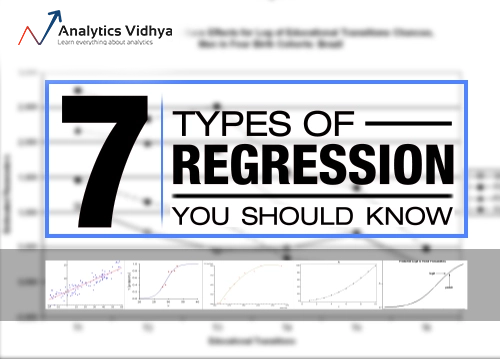
Lecture 11 Matrix Approach to Linear Regression. Bivariate and multivariate analyses are statistical methods to investigate relationships between data samples. Bivariate analysis looks at two paired data sets, studying whether a relationship exists between them. Multivariate analysis uses two or more variables and analyzes which, if any, are correlated with a specific outcome. The goal in the, Fittingalinearmodel 0 5 101520 25 30 Cigarettes smoked per day 600 700 800 900 CVD deaths1000 CVD deaths for different smoking intensities import numpy, pandas.

RegressIt Free Excel regression add-in for PCs and Macs

Applied Regression Analysis A Research Tool Second Edition. Set Up Multivariate Regression Problems. To fit a multivariate linear regression model using mvregress, you must set up your response matrix and design matrices in a particular way.. Multivariate General Linear Model. This example shows how to set up a multivariate general linear model for estimation using mvregress.. Fixed Effects Panel Model with Concurrent Correlation 16.0 Multiple and Nonlinear Regression • Answer Questions • Multiple Regression • Nonlinear Regression • Regression 1. 16.1 Multiple Regression Recall the regression assumptions: 1. Each point (X i,Y i) in the scatterplot satisfies: Y i = β0 +β1X i +ǫ i where the ǫ i have a normal distribution with mean zero and (usually) unknown standard deviation. 2. The errors ǫ i have nothing.

Regression analysis of variance table page 18 Here is the layout of the analysis of variance table associated with regression. There is some simple structure to this table. Several of the important quantities associated with the regression are obtained directly from the analysis of variance table. Indicator variables page 20 Special techniques are needed in dealing with non-ordinal categorical Multivariate Behavi Applied Regression Analysis Norman R Draper Harry Smith Pdf Green, S. B. (1991). How Many Subjects Does It Take To Do A Regression Analysis? Multivariate Behavi Multiple Linear Regression Analysis Model Adequacy Statistics Using Stata Time Series Analysis And Its Applications With R Examples

multiple linear regression analysis. Review of lecture two weeks ago • Linear regression assumes a linear relationship between independent variable(s) and dependent variable • Linear regression allows us to predict an outcome based on one or several predictors • Linear regression allows us to explain the interrelationships among variables • Linear regression is a parametric test. How Multivariate Linear Regression Nathaniel E. Helwig Assistant Professor of Psychology and Statistics University of Minnesota (Twin Cities) Updated 16-Jan-2017 Nathaniel E. Helwig (U of Minnesota) Multivariate Linear Regression Updated 16-Jan-2017 : Slide 1

Another term, multivariate linear regression, refers to cases where y is a vector, i.e., the same as general linear regression. General linear models. The general linear model considers the situation when the response variable is not a scalar (for each observation) but a vector, y i. Multivariate Analysis: Linear Regression What factors influence confidence in the police? Remember that we are using the Crime Survey for England and Wales (CSEW), which is a large-scale survey conducted each year in an effort to better understand public experiences with crime and the police.

Bivariate and multivariate analyses are statistical methods to investigate relationships between data samples. Bivariate analysis looks at two paired data sets, studying whether a relationship exists between them. Multivariate analysis uses two or more variables and analyzes which, if any, are correlated with a specific outcome. The goal in the • You use correlation analysis to find out if there is a statistically significant relationship between TWO variables. • You use linear regression analysis to make predictions based on the relationship that exists between two variables. The main limitation that you have with correlation and linear regression …

Linear regression for the advertising data Consider the advertising data shown on the next slide. Questions we might ask: Is there a relationship between advertising budget and 5.6.2 Obtaining T2 from Multiple Regression, 130 5.7 Paired Observations Test, 132 5.7.1 Univariate Case, 132 5.7.2 Multivariate Case, 134 5.8 Test for Additional Information, 136 5.9 Profile Analysis, 139 5.9.1 One-Sample Profile Analysis, 139 5.9.2 Two-Sample Profile Analysis, 141 6. Multivariate Analysis of Variance 156 6.1 One-Way Models

Multivariate Linear Regression Nathaniel E. Helwig Assistant Professor of Psychology and Statistics University of Minnesota (Twin Cities) Updated 16-Jan-2017 Nathaniel E. Helwig (U of Minnesota) Multivariate Linear Regression Updated 16-Jan-2017 : Slide 1 5.6.2 Obtaining T2 from Multiple Regression, 130 5.7 Paired Observations Test, 132 5.7.1 Univariate Case, 132 5.7.2 Multivariate Case, 134 5.8 Test for Additional Information, 136 5.9 Profile Analysis, 139 5.9.1 One-Sample Profile Analysis, 139 5.9.2 Two-Sample Profile Analysis, 141 6. Multivariate Analysis of Variance 156 6.1 One-Way Models

= Multiple linear regression = T-test = Univar. classification trees ANOVA = Univar. regression trees = Analysis of variance = Hotelling’s T 2 = Multivariate analysis of variance = Discriminant analysis = Indicator species analysis = Redundancy analysis = Can. correspond. analysis = Multivar. regression trees = Canonical corr. analysis CAP = Can. prin. coord. analysis Dependence Techniques Multiple Regression Analysis Let z1;z2;:::;zrbe a set of rpredictors believed to be related to a response variable Y. The linear regression model for the jth sample unit has the form Yj= 0 + 1zj1 + 2zj2 + :::+ rzjr+ j; where is a random error and the i;i= 0;1;:::;r are un-known (and xed) regression coe cients.

Frank Wood, fwood@stat.columbia.edu Linear Regression Models Lecture 11, Slide 20 Hat Matrix – Puts hat on Y • We can also directly express the fitted values in terms of only the X and Y matrices and we can further define H, the “hat matrix” • The hat matrix plans an important role in diagnostics for regression analysis. write H on board Linear Regression as a Statistical Model 5. Multiple Linear Regression and Matrix Formulation CHAPTER 1: Basic Concepts of Regression Analysis Prof. Alan Wan 1/42. 1. Introduction 2. Approaches to Line Fitting 3. The Least Squares Approach 4. Linear Regression as a Statistical Model 5. Multiple Linear Regression and Matrix Formulation Table of contents 1. Introduction 2. Approaches to Line

= Multiple linear regression = T-test = Univar. classification trees ANOVA = Univar. regression trees = Analysis of variance = Hotelling’s T 2 = Multivariate analysis of variance = Discriminant analysis = Indicator species analysis = Redundancy analysis = Can. correspond. analysis = Multivar. regression trees = Canonical corr. analysis CAP = Can. prin. coord. analysis Dependence Techniques 5 IBM SPSS Statistics 23 Part 3: Regression Analysis Predicting Values of Dependent Variables Judging from the scatter plot above, a linear relationship seems to exist between the two variables. Therefore, a simple regression analysis can be used to calculate an equation that will help predict this year’s sales.

5 IBM SPSS Statistics 23 Part 3: Regression Analysis Predicting Values of Dependent Variables Judging from the scatter plot above, a linear relationship seems to exist between the two variables. Therefore, a simple regression analysis can be used to calculate an equation that will help predict this year’s sales. Multiple Linear Regression The population model • In a simple linear regression model, a single response measurement Y is related to a single predictor (covariate, regressor) X for each observation. The critical assumption of the model is that the conditional mean function is linear: E(Y|X) = α +βX.

Multiple Linear Regression The population model • In a simple linear regression model, a single response measurement Y is related to a single predictor (covariate, regressor) X for each observation. The critical assumption of the model is that the conditional mean function is linear: E(Y|X) = α +βX. • Linear vs non-linear • Non linear regression analysis Research in Pharmacoepidemiology (RIPE) @ National School of Pharmacy, University of Otago. Linear regression (reminder) • Linear regression is an approach for modelling dependent variable( ) and one or more explanatory variables ( ). =𝛽0+𝛽1 +𝜀 Assumptions: 𝜀~𝑁(0,𝜎2) –iid ( independently identically distributed