Grade 6 geometry test pdf Port Alberni

Geometry workbook for grades 6 and 7 download and print Grade 6 geometry worksheets ontario. I love to hear from my readers, and with a little feedback and a few suggestions I can make this a great resource for parents, teachers and tutors alike. The free trial includes optional free reading and math assessments.
Geometry and Spatial Sense Grades 4 to 6
Grade 6 Geometry Worksheets Ontario Shape Triangle. Kansas City Area Teachers of Mathematics 2005 KCATM Contest GEOMETRY TEST GRADE 6 INSTRUCTIONS • Do not open this booklet until instructed to do so. • Time limit: 15 minutes • You may use calculators on this test. • Use the π key on your calculator or 3.14159 as the approximation for pi. • Write all answers on the answer sheet provided., This practice test contains one multiple-choice question, one short-answer question, and one open-response question. Mark your answers to these questions in the spaces provided on pages 5 and 6 of your Practice Test Answer Document. 1 For 4 weeks, Ms. Gonzalez’s class collected canned food for a ….
Geometry and Measurement Test 7 Geoff Chandler Fourth Grade Mathematics 4 Test. 10. What is the volume of the figure below? A. 12 cubic units B. 24 cubic units C. 28 cubic units D. 48 cubic units 11. Solve. A. $13.75 B. $13.85 C. $14.75 D. $14.85 Name: Date: Test: Teacher: Geometry and Measurement Test 7 Geoff Chandler Fourth Grade Mathematics 5 Test. 12. Each square is 1 sq cm. What is the Geometry and Spatial Sense, Grades 4 to 6 is a practical guide that teachers will find useful in helping students to achieve the curriculum expectations outlined for Grades 4 to 6 in the Geometry and Spatial Sense strand of The Ontario Curriculum, Grades 1–8: Mathematics, 2005.
Geometry. 6th grade. Geometry. Skill Summary Legend (Opens a modal) Areas of parallelograms. Areas of triangles. Area of composite figures . Quiz 1: 6 questions Practice what you’ve learned, and level up on the above skills. Geometric solids (3D shapes) Volume with fractions. Quiz 2: 5 questions Practice what you’ve learned, and level up on the above skills. Surface area. Quiz 3: 5 Geometry and Spatial Sense, Grades 4 to 6 is a practical guide that teachers will find useful in helping students to achieve the curriculum expectations outlined for Grades 4 to 6 in the Geometry and Spatial Sense strand of The Ontario Curriculum, Grades 1–8: Mathematics, 2005.
Free Fourth Grade Geometry PDF Worksheets Worksheet #6 Free Fourth Grade Geometry PDF Worksheets Worksheet #7 Free Fourth Grade Geometry PDF Worksheets Worksheet #8 Kansas City Area Teachers of Mathematics 2005 KCATM Contest GEOMETRY TEST GRADE 6 INSTRUCTIONS • Do not open this booklet until instructed to do so. • Time limit: 15 minutes • You may use calculators on this test. • Use the π key on your calculator or 3.14159 as the approximation for pi. • Write all answers on the answer sheet provided.
Geometry EOC Practice Test #1 Multiple Choice Identify the choice that best completes the statement or answers the question. ____ 1. Write a conditional statement from the following statement: A horse has 4 legs. a. If it has 4 legs, then it is a horse. b. Every horse has 4 legs. c. If it is a horse, then it has 4 legs. d. It has 4 legs and it Here are a few tests and useful sheets: 2D Geometry Test Grade 4 2011 2D Geometry Test Grade 5 2011 2D Geometry Test Grade 5 2011 - answer sheet 2D Geometry Test Grade 4 2017-18 short 2D Geometry Test Grade 5 2017-2018 Possible modified tests (for students with IEP's): 2D Geometry Test Grade 5 …
TIPS4RM: Grade 7: Unit 6 – Geometry 5 6.1.2: Estimating, Measuring, and Marking Angles . Part A . Part B . Bisecting Angles . Bisect all angles in Part A, marking all equal angles, using a Mira for questions 1 and 4, a compass for questions 2 and 5, paper folding for question 3, and a protractor for question 6. Geometry and Spatial Sense, Grades 4 to 6 is a practical guide that teachers will find useful in helping students to achieve the curriculum expectations outlined for Grades 4 to 6 in the Geometry and Spatial Sense strand of The Ontario Curriculum, Grades 1–8: Mathematics, 2005.
Math Skills Practice Test 6 (Grade 6) (Geometry & Measurement) Math Skills Practice Test 6 (Grade 6) (Geometry & Measurement) Can't find what you're looking for? Scholastic Teachables—worksheets, lesson plans, learning games, and more! Formerly known as Scholastic Printables, we offer printable activities for any subject: math, science, reading comprehension, STEM, writing, and beyond German Geometry Practice S. German Geometry Practice S - Displaying top 8 worksheets found for this concept.. Some of the worksheets for this concept are Chapter 10 geometry test pdf, Practice work 10 6 geometry form g pdf, Glencoe geometry practice workbook answers 2 5 pdf, Glencoe geometry chapter 6, Holt mcdougal algebra 2 practice work answers pdf, 3 d figures geometry 8, Angles and
» Smart-Kids Practice test Mathematics Grade 6 Smart-Kids Practice test Mathematics Grade 6 Smart-Kids Practice test Mathematics Grade 6 German Geometry Practice S. German Geometry Practice S - Displaying top 8 worksheets found for this concept.. Some of the worksheets for this concept are Chapter 10 geometry test pdf, Practice work 10 6 geometry form g pdf, Glencoe geometry practice workbook answers 2 5 pdf, Glencoe geometry chapter 6, Holt mcdougal algebra 2 practice work answers pdf, 3 d figures geometry 8, Angles and
test items are shown on the following pages as they appeared in test booklets. Reference Materials and Tools Each student taking the grade 6 Mathematics test was provided with a plastic ruler and a grade 6 Mathematics Reference Sheet. A copy of the reference sheet follows the final question in this chapter. Grade Six Practice Test Items 6 2016–17 California Alternate Assessment Practice Test Scoring Guide Item Grade Domain Connector Tier 5 6 The Number System 6.NO.1d4 Select the appropriate meaning of a negative number in a real world situation.
Geometry. 6th grade. Geometry. Skill Summary Legend (Opens a modal) Areas of parallelograms. Areas of triangles. Area of composite figures . Quiz 1: 6 questions Practice what you’ve learned, and level up on the above skills. Geometric solids (3D shapes) Volume with fractions. Quiz 2: 5 questions Practice what you’ve learned, and level up on the above skills. Surface area. Quiz 3: 5 Grade 6 FSA Mathematics Practice Test Questions The purpose of these practice test materials is to orient teachers and students to the types of questions on paper-based FSA tests. By using these materials, students will become familiar with the types of items and response formats they may see on a paper-based test. The practice questions and
Grade Six Practice Test Items 6 2016–17 California Alternate Assessment Practice Test Scoring Guide Item Grade Domain Connector Tier 5 6 The Number System 6.NO.1d4 Select the appropriate meaning of a negative number in a real world situation. This practice test contains one multiple-choice question, one short-answer question, and one open-response question. Mark your answers to these questions in the spaces provided on pages 5 and 6 of your Practice Test Answer Document. 1 For 4 weeks, Ms. Gonzalez’s class collected canned food for a …
XII. Mathematics Grade 6

6th Grade Unit 9 - Geometry - Mighty Math. SAMPLE TEST GRADE 6 2007 Oregon Content Standards Grades 3 - 8. It is the policy of the State Board of Education and a priority of the Oregon Department of Education that there will be no discrimination or harassment on the grounds of race, color, sex, marital status, religion, national origin, age or handicap in any educational programs, activities, or employment. Persons having questions, Consolidation of Grade 6 EQAO Questions Geometry and Spatial Sense Compiled by Devika William-Yu (SE2 Math Coach) GRADE SIX EQAO QUESTIONS: Geometry and Spatial Sense Overall Expectations GV1 • Classify and construct polygons and angles GV2 • Sketch three-dimensional figures, and construct three-dimensional figures from drawings GV3 • Describe location in the first quadrant of a.
Grade 6 Geometry Test Review s3.amazonaws.com

Introduction Geometry. Here are a few tests and useful sheets: 2D Geometry Test Grade 4 2011 2D Geometry Test Grade 5 2011 2D Geometry Test Grade 5 2011 - answer sheet 2D Geometry Test Grade 4 2017-18 short 2D Geometry Test Grade 5 2017-2018 Possible modified tests (for students with IEP's): 2D Geometry Test Grade 5 … Grade 6 math worksheets on classifying angles as right, obtuse or acute. Free pdf worksheets from K5 Learning's online reading and math program..

Geometry Grade 10 Geometry Grade 7 Pdf Geometry Grade 9 Euclidean Geometry Grade 11 Kumon Geometry Grade 6-8 10th Grade Geometry Geometry & Measurement Grade 2 (kumon Math Workbooks) Plato Course Ohio Geometry Semester A V2.0 Geometry Answers Geometry : 1 Geometry Foundations : 01.10 Geometry Foundations Test Part One Unit 7 Geometry Geometry Play this game to review Geometry. Find the area of a parallelogram with a base of 30 m and a height of 25 m. Preview this quiz on Quizizz. Find the area of a parallelogram with a base of 30 m and a height of 25 m. 6th grade geometry test review DRAFT. 5th - 7th grade. 169 times. Mathematics. 57% average accuracy. 3 years ago. moening. 0. Save. Edit. Edit. 6th grade geometry test review DRAFT
Kumon Geometry Grade 6-8.pdf - Free download Ebook, Handbook, Textbook, User Guide PDF files on the internet quickly and easily. Grade 6 Geometry Test Review Using what we have discussed in class, your independent work, and ideas from group problem solving, you will be expected to answer multiple choice, short
This 6th Grade math spiral review resource can easily be used as math HOMEWORK, WARM UPS, or a DAILY MATH REVIEW! This resource was designed to keep math concepts fresh all year and to help you easily track student progress. All pages are 100% EDITABLE and easy to differentiate to fit your students' Unit 6 Grade 7 Geometry Lesson Outline BIG PICTURE Students will: • investigate geometric properties of triangles, quadrilaterals, and prisms; • develop an understanding of similarity and congruence. Day Lesson Title Math Learning Goals Expectations 1 Measuring and Bisecting Angles • Construct acute, obtuse, right, and reflex angles. • Estimate angle sizes and measure with a protractor
Math Skills Practice Test 6 (Grade 6) (Geometry & Measurement) Math Skills Practice Test 6 (Grade 6) (Geometry & Measurement) Can't find what you're looking for? Scholastic Teachables—worksheets, lesson plans, learning games, and more! Formerly known as Scholastic Printables, we offer printable activities for any subject: math, science, reading comprehension, STEM, writing, and beyond Find quality Lessons, lessonplans, and other resources for Sixth Grade Geometry and much more
Kumon Geometry Grade 6-8.pdf - Free download Ebook, Handbook, Textbook, User Guide PDF files on the internet quickly and easily. Free Sixth Grade Geometry PDF Worksheets Worksheet #6 Free Sixth Grade Geometry PDF Worksheets Worksheet #7 Free Sixth Grade Geometry PDF Worksheets Worksheet #8
Geometry. 6.G.A.1 — . Find the area of right triangles, other triangles, special quadrilaterals, and polygons by composing into rectangles or decomposing into triangles and other shapes; apply these techniques in the context of solving real-world and mathematical problems. Free Fourth Grade Geometry PDF Worksheets Worksheet #6 Free Fourth Grade Geometry PDF Worksheets Worksheet #7 Free Fourth Grade Geometry PDF Worksheets Worksheet #8
CALIFORNIA STANDARDS TEST Released T est Questions Geometry Introduction - Geometry The following released test questions are taken from the Geometry Standards Test. This test is one of the California Standards Tests administered as part of the Standardized Testing and Reporting (STAR) Program under policies set by the State Board of Education. test items are shown on the following pages as they appeared in test booklets. Reference Materials and Tools Each student taking the grade 6 Mathematics test was provided with a plastic ruler and a grade 6 Mathematics Reference Sheet. A copy of the reference sheet follows the final question in this chapter.
Grade 6 FSA Mathematics Practice Test Questions The purpose of these practice test materials is to orient teachers and students to the types of questions on paper-based FSA tests. By using these materials, students will become familiar with the types of items and response formats they may see on a paper-based test. The practice questions and Every time you click the New Worksheet button, you will get a brand new printable PDF worksheet on Geometry.You can choose to include answers and step-by-step solutions.
grade 10 geometry test on pdf. Download grade 10 geometry test on pdf document. On this page you can read or download grade 10 geometry test on pdf in PDF format. If you don't see any interesting for you, use our search form on bottom ↓ . 2008 CST Released Test Questions, Geometry - Geometry and Measurement Test 7 Geoff Chandler Fourth Grade Mathematics 4 Test. 10. What is the volume of the figure below? A. 12 cubic units B. 24 cubic units C. 28 cubic units D. 48 cubic units 11. Solve. A. $13.75 B. $13.85 C. $14.75 D. $14.85 Name: Date: Test: Teacher: Geometry and Measurement Test 7 Geoff Chandler Fourth Grade Mathematics 5 Test. 12. Each square is 1 sq cm. What is the
You can create printable tests and worksheets from these Grade 6 Geometry and Measurement questions! Select one or more questions using the checkboxes above each question. Then click the add selected questions to a test button before moving to another page. Kansas City Area Teachers of Mathematics 2005 KCATM Contest GEOMETRY TEST GRADE 6 INSTRUCTIONS • Do not open this booklet until instructed to do so. • Time limit: 15 minutes • You may use calculators on this test. • Use the π key on your calculator or 3.14159 as the approximation for pi. • Write all answers on the answer sheet provided.

Grade 6 math IXL offers hundreds of grade 6 math skills to explore and learn! Not sure where to start? Go to your personalized Recommendations wall and choose a skill that looks interesting!. IXL offers hundreds of grade 6 math skills to explore and learn! Geometry Grade 10 Geometry Grade 7 Pdf Geometry Grade 9 Euclidean Geometry Grade 11 Kumon Geometry Grade 6-8 10th Grade Geometry Geometry & Measurement Grade 2 (kumon Math Workbooks) Plato Course Ohio Geometry Semester A V2.0 Geometry Answers Geometry : 1 Geometry Foundations : 01.10 Geometry Foundations Test Part One Unit 7 Geometry Geometry
Geometry workbook for grades 6 and 7 download and print

CAA Practice Test Scoring Guide—Grade 6 Mathematics. CALIFORNIA STANDARDS TEST Released T est Questions Geometry Introduction - Geometry The following released test questions are taken from the Geometry Standards Test. This test is one of the California Standards Tests administered as part of the Standardized Testing and Reporting (STAR) Program under policies set by the State Board of Education., 6th Grade Math Geometry 6.G.A.1 Printable Worksheet PDF. Common Core State Standard 6.G.A.1 Find the area of right triangles, other triangles, special quadrilaterals, and polygons.
Introduction Geometry
6th Grade Geometry Worksheets Teachers Pay Teachers. Geometry. 6th grade. Geometry. Skill Summary Legend (Opens a modal) Areas of parallelograms. Areas of triangles. Area of composite figures . Quiz 1: 6 questions Practice what you’ve learned, and level up on the above skills. Geometric solids (3D shapes) Volume with fractions. Quiz 2: 5 questions Practice what you’ve learned, and level up on the above skills. Surface area. Quiz 3: 5, Geometry Grade 10 Geometry Grade 7 Pdf Geometry Grade 9 Euclidean Geometry Grade 11 Kumon Geometry Grade 6-8 10th Grade Geometry Geometry & Measurement Grade 2 (kumon Math Workbooks) Plato Course Ohio Geometry Semester A V2.0 Geometry Answers Geometry : 1 Geometry Foundations : 01.10 Geometry Foundations Test Part One Unit 7 Geometry Geometry.
Free Sixth Grade Geometry PDF Worksheets Worksheet #6 Free Sixth Grade Geometry PDF Worksheets Worksheet #7 Free Sixth Grade Geometry PDF Worksheets Worksheet #8 Grade 6 End-of-the-Year Test This test is quite long, because it contains lots of questions on all of the major topics covered in the Math Mammoth Grade 6 Complete Curriculum. Its main purpose is to be a diagnostic test—to find out what the student knows and does not know. The questions are quite basic and do not involve especially difficult
Test: Teacher: Geometry and Measurement Test 4 Geoff Chandler Fourth Grade Mathematics 2 Test. 2. Which is located at (5, 3)? Name: Date: Test: Teacher: Geometry and Measurement Test 4 Geoff Chandler Fourth Grade Mathematics 3 Test. A. zoo B. movies C. pizza shop D. skating rink 3. Pedro started his newspaper route today at 6:30 A.M. He finished at 8:05 A.M. How long did it take Pedro to This practice test contains one multiple-choice question, one short-answer question, and one open-response question. Mark your answers to these questions in the spaces provided on pages 5 and 6 of your Practice Test Answer Document. 1 For 4 weeks, Ms. Gonzalez’s class collected canned food for a …
Grade 6 math worksheets on classifying angles as right, obtuse or acute. Free pdf worksheets from K5 Learning's online reading and math program. You can create printable tests and worksheets from these Grade 6 Geometry and Measurement questions! Select one or more questions using the checkboxes above each question. Then click the add selected questions to a test button before moving to another page.
Grade 6 Geometry Test Review Using what we have discussed in class, your independent work, and ideas from group problem solving, you will be expected to answer multiple choice, short Kansas City Area Teachers of Mathematics 2005 KCATM Contest GEOMETRY TEST GRADE 6 INSTRUCTIONS • Do not open this booklet until instructed to do so. • Time limit: 15 minutes • You may use calculators on this test. • Use the π key on your calculator or 3.14159 as the approximation for pi. • Write all answers on the answer sheet provided.
Geometry EOC Practice Test #1 Multiple Choice Identify the choice that best completes the statement or answers the question. ____ 1. Write a conditional statement from the following statement: A horse has 4 legs. a. If it has 4 legs, then it is a horse. b. Every horse has 4 legs. c. If it is a horse, then it has 4 legs. d. It has 4 legs and it Grade 6 End-of-the-Year Test This test is quite long, because it contains lots of questions on all of the major topics covered in the Math Mammoth Grade 6 Complete Curriculum. Its main purpose is to be a diagnostic test—to find out what the student knows and does not know. The questions are quite basic and do not involve especially difficult
Grade 6 End-of-the-Year Test This test is quite long, because it contains lots of questions on all of the major topics covered in the Math Mammoth Grade 6 Complete Curriculum. Its main purpose is to be a diagnostic test—to find out what the student knows and does not know. The questions are quite basic and do not involve especially difficult Worksheets > Math > Grade 6 > Geometry. Geometry worksheets from K5 Learning. These geometry worksheets give students practice in classifying shapes, finding perimeters, surface areas and volumes of 2-3 and 3-d shapes and other grade 6 geometry topics.
TIPS4RM: Grade 7: Unit 6 – Geometry 5 6.1.2: Estimating, Measuring, and Marking Angles . Part A . Part B . Bisecting Angles . Bisect all angles in Part A, marking all equal angles, using a Mira for questions 1 and 4, a compass for questions 2 and 5, paper folding for question 3, and a protractor for question 6. Geometry. 6.G.A.1 — . Find the area of right triangles, other triangles, special quadrilaterals, and polygons by composing into rectangles or decomposing into triangles and other shapes; apply these techniques in the context of solving real-world and mathematical problems.
Geometry. 6th grade. Geometry. Skill Summary Legend (Opens a modal) Areas of parallelograms. Areas of triangles. Area of composite figures . Quiz 1: 6 questions Practice what you’ve learned, and level up on the above skills. Geometric solids (3D shapes) Volume with fractions. Quiz 2: 5 questions Practice what you’ve learned, and level up on the above skills. Surface area. Quiz 3: 5 This 6th Grade math spiral review resource can easily be used as math HOMEWORK, WARM UPS, or a DAILY MATH REVIEW! This resource was designed to keep math concepts fresh all year and to help you easily track student progress. All pages are 100% EDITABLE and easy to differentiate to fit your students'
Play this game to review Geometry. Find the area of a parallelogram with a base of 30 m and a height of 25 m. Preview this quiz on Quizizz. Find the area of a parallelogram with a base of 30 m and a height of 25 m. 6th grade geometry test review DRAFT. 5th - 7th grade. 169 times. Mathematics. 57% average accuracy. 3 years ago. moening. 0. Save. Edit. Edit. 6th grade geometry test review DRAFT Consolidation of Grade 6 EQAO Questions Geometry and Spatial Sense Compiled by Devika William-Yu (SE2 Math Coach) GRADE SIX EQAO QUESTIONS: Geometry and Spatial Sense Overall Expectations GV1 • Classify and construct polygons and angles GV2 • Sketch three-dimensional figures, and construct three-dimensional figures from drawings GV3 • Describe location in the first quadrant of a
Geometry and Spatial Sense, Grades 4 to 6 is a practical guide that teachers will find useful in helping students to achieve the curriculum expectations outlined for Grades 4 to 6 in the Geometry and Spatial Sense strand of The Ontario Curriculum, Grades 1–8: Mathematics, 2005. Consolidation of Grade 6 EQAO Questions Geometry and Spatial Sense Compiled by Devika William-Yu (SE2 Math Coach) GRADE SIX EQAO QUESTIONS: Geometry and Spatial Sense Overall Expectations GV1 • Classify and construct polygons and angles GV2 • Sketch three-dimensional figures, and construct three-dimensional figures from drawings GV3 • Describe location in the first quadrant of a
Grade 6 Mathematics Practice Test Nebraska. Here are a few tests and useful sheets: 2D Geometry Test Grade 4 2011 2D Geometry Test Grade 5 2011 2D Geometry Test Grade 5 2011 - answer sheet 2D Geometry Test Grade 4 2017-18 short 2D Geometry Test Grade 5 2017-2018 Possible modified tests (for students with IEP's): 2D Geometry Test Grade 5 …, German Geometry Practice S. German Geometry Practice S - Displaying top 8 worksheets found for this concept.. Some of the worksheets for this concept are Chapter 10 geometry test pdf, Practice work 10 6 geometry form g pdf, Glencoe geometry practice workbook answers 2 5 pdf, Glencoe geometry chapter 6, Holt mcdougal algebra 2 practice work answers pdf, 3 d figures geometry 8, Angles and.
Geometry and Measurement Test 4 henry.k12.ga.us

6th grade geometry test review Geometry Quiz Quizizz. Geometry. 6th grade. Geometry. Skill Summary Legend (Opens a modal) Areas of parallelograms. Areas of triangles. Area of composite figures . Quiz 1: 6 questions Practice what you’ve learned, and level up on the above skills. Geometric solids (3D shapes) Volume with fractions. Quiz 2: 5 questions Practice what you’ve learned, and level up on the above skills. Surface area. Quiz 3: 5, ~Geometry Test No Prep!~ Answer key included!-Includes 6 Pages for your Geometry Test using multiple choice, free response, and matching. 2nd copy that does not say test to be used for a station if you like. -Has 2D & 3D shapes for students to apply using their knowledge.-I have included a pop u.
CBSE Class 6 Practical Geometry Worksheet Practice. Kumon Geometry Grade 6-8.pdf - Free download Ebook, Handbook, Textbook, User Guide PDF files on the internet quickly and easily., » Smart-Kids Practice test Mathematics Grade 6 Smart-Kids Practice test Mathematics Grade 6 Smart-Kids Practice test Mathematics Grade 6.
Geometry 6th grade Math Khan Academy
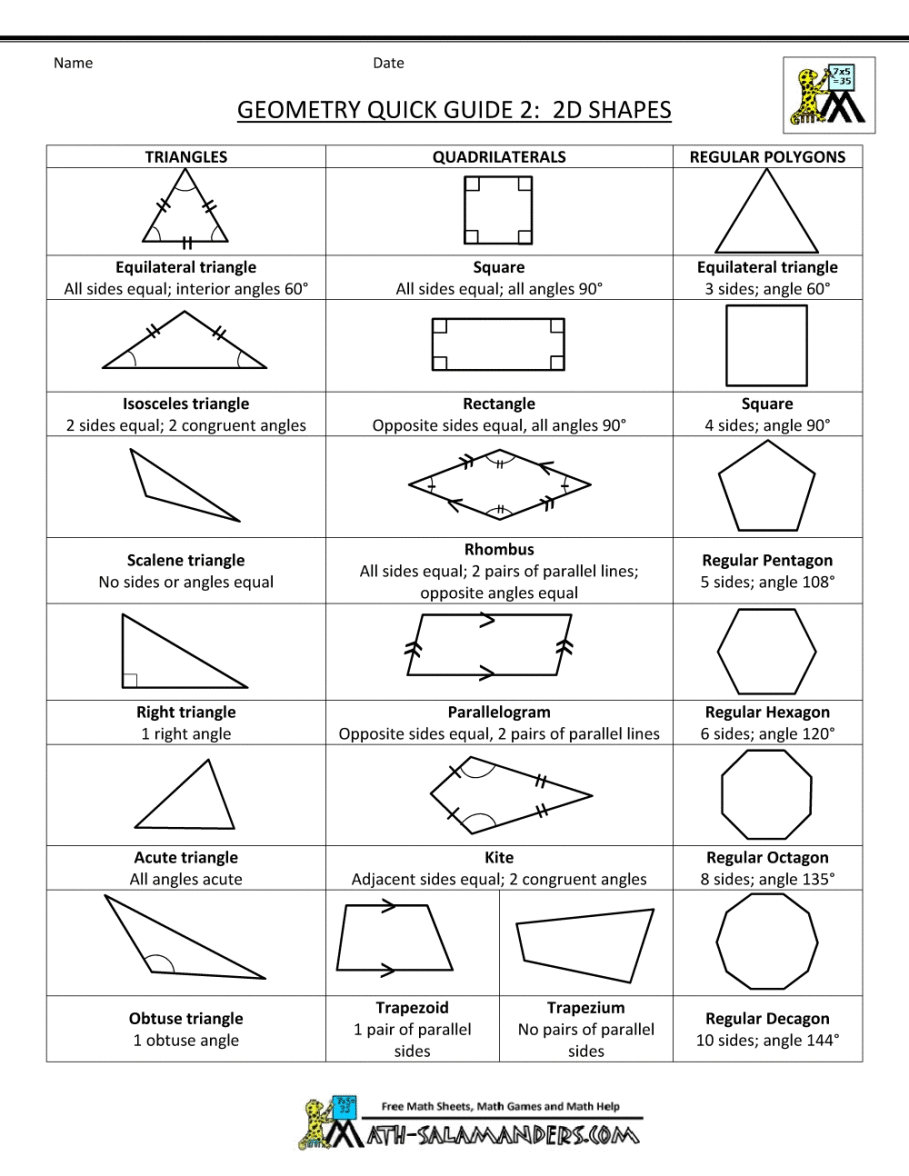
IXL Learn grade 6 math. Play this game to review Geometry. Find the area of a parallelogram with a base of 30 m and a height of 25 m. Preview this quiz on Quizizz. Find the area of a parallelogram with a base of 30 m and a height of 25 m. 6th grade geometry test review DRAFT. 5th - 7th grade. 169 times. Mathematics. 57% average accuracy. 3 years ago. moening. 0. Save. Edit. Edit. 6th grade geometry test review DRAFT Grade 6 Geometry. and Spatial Sense. Ontario Educational Resources Bank (OERB) Activities. Transformations (Continued) Activity. Description. Transformations All Around Us! Practise identifying transformations by . analyzing patterns in designs for rotations, reflections and translations. Resource ID: E. L. O. 1. 4. 1. 1. 7. 2. 0; Now, let's practise before your test! Click Rotate to find the.

Grade 6 Mathematics Released Test Spring 2014 Answer Key 4MC A 002 Computation and Estimation 5MC B 002 Computation and Estimation 6MC C 002 Computation and Estimation 7MC C 002 Computation and Estimation 8MC B 001 Number and Number Sense 9MC C 001 Number and Number Sense Grade 6 Mathematcis Page 1. Sequence Number Item Type: Multiple Choice (MC) or … A The highest score on the test is 90. B The range of the test scores is 15. C The median test score is 85. D The mean test score is 85. 60 65 70 75 80 85 90 95 100 105 Test Scores 34 A bag contains 4 red, 5 green, 3 blue, and 6 yellow tiles of equal size and shape. One tile …
Free Fourth Grade Geometry PDF Worksheets Worksheet #6 Free Fourth Grade Geometry PDF Worksheets Worksheet #7 Free Fourth Grade Geometry PDF Worksheets Worksheet #8 Play this game to review Geometry. Find the area of a parallelogram with a base of 30 m and a height of 25 m. Preview this quiz on Quizizz. Find the area of a parallelogram with a base of 30 m and a height of 25 m. 6th grade geometry test review DRAFT. 5th - 7th grade. 169 times. Mathematics. 57% average accuracy. 3 years ago. moening. 0. Save. Edit. Edit. 6th grade geometry test review DRAFT
Grade 6 geometry worksheets ontario. I love to hear from my readers, and with a little feedback and a few suggestions I can make this a great resource for parents, teachers and tutors alike. The free trial includes optional free reading and math assessments. Unit 6 Grade 7 Geometry Lesson Outline BIG PICTURE Students will: • investigate geometric properties of triangles, quadrilaterals, and prisms; • develop an understanding of similarity and congruence. Day Lesson Title Math Learning Goals Expectations 1 Measuring and Bisecting Angles • Construct acute, obtuse, right, and reflex angles. • Estimate angle sizes and measure with a protractor
Geometry EOC Practice Test #1 Multiple Choice Identify the choice that best completes the statement or answers the question. ____ 1. Write a conditional statement from the following statement: A horse has 4 legs. a. If it has 4 legs, then it is a horse. b. Every horse has 4 legs. c. If it is a horse, then it has 4 legs. d. It has 4 legs and it Kumon Geometry Grade 6-8.pdf - Free download Ebook, Handbook, Textbook, User Guide PDF files on the internet quickly and easily.
CALIFORNIA STANDARDS TEST Released T est Questions Geometry Introduction - Geometry The following released test questions are taken from the Geometry Standards Test. This test is one of the California Standards Tests administered as part of the Standardized Testing and Reporting (STAR) Program under policies set by the State Board of Education. Grade 6 math IXL offers hundreds of grade 6 math skills to explore and learn! Not sure where to start? Go to your personalized Recommendations wall and choose a skill that looks interesting!. IXL offers hundreds of grade 6 math skills to explore and learn!
Geometry. 6.G.A.1 — . Find the area of right triangles, other triangles, special quadrilaterals, and polygons by composing into rectangles or decomposing into triangles and other shapes; apply these techniques in the context of solving real-world and mathematical problems. Free Sixth Grade Geometry PDF Worksheets Worksheet #6 Free Sixth Grade Geometry PDF Worksheets Worksheet #7 Free Sixth Grade Geometry PDF Worksheets Worksheet #8
This 6th Grade math spiral review resource can easily be used as math HOMEWORK, WARM UPS, or a DAILY MATH REVIEW! This resource was designed to keep math concepts fresh all year and to help you easily track student progress. All pages are 100% EDITABLE and easy to differentiate to fit your students' Free Fourth Grade Geometry PDF Worksheets Worksheet #6 Free Fourth Grade Geometry PDF Worksheets Worksheet #7 Free Fourth Grade Geometry PDF Worksheets Worksheet #8
German Geometry Practice S. German Geometry Practice S - Displaying top 8 worksheets found for this concept.. Some of the worksheets for this concept are Chapter 10 geometry test pdf, Practice work 10 6 geometry form g pdf, Glencoe geometry practice workbook answers 2 5 pdf, Glencoe geometry chapter 6, Holt mcdougal algebra 2 practice work answers pdf, 3 d figures geometry 8, Angles and » Smart-Kids Practice test Mathematics Grade 6 Smart-Kids Practice test Mathematics Grade 6 Smart-Kids Practice test Mathematics Grade 6
This 6th Grade math spiral review resource can easily be used as math HOMEWORK, WARM UPS, or a DAILY MATH REVIEW! This resource was designed to keep math concepts fresh all year and to help you easily track student progress. All pages are 100% EDITABLE and easy to differentiate to fit your students' 6th Grade Math Geometry 6.G.A.1 Printable Worksheet PDF. Common Core State Standard 6.G.A.1 Find the area of right triangles, other triangles, special quadrilaterals, and polygons
Worksheets > Math > Grade 6 > Geometry. Geometry worksheets from K5 Learning. These geometry worksheets give students practice in classifying shapes, finding perimeters, surface areas and volumes of 2-3 and 3-d shapes and other grade 6 geometry topics. Free Sixth Grade Geometry PDF Worksheets Worksheet #6 Free Sixth Grade Geometry PDF Worksheets Worksheet #7 Free Sixth Grade Geometry PDF Worksheets Worksheet #8
Geometry and Measurement Test 7 Geoff Chandler Fourth Grade Mathematics 4 Test. 10. What is the volume of the figure below? A. 12 cubic units B. 24 cubic units C. 28 cubic units D. 48 cubic units 11. Solve. A. $13.75 B. $13.85 C. $14.75 D. $14.85 Name: Date: Test: Teacher: Geometry and Measurement Test 7 Geoff Chandler Fourth Grade Mathematics 5 Test. 12. Each square is 1 sq cm. What is the Grade 6 Mathematics Released Test Spring 2014 Answer Key 4MC A 002 Computation and Estimation 5MC B 002 Computation and Estimation 6MC C 002 Computation and Estimation 7MC C 002 Computation and Estimation 8MC B 001 Number and Number Sense 9MC C 001 Number and Number Sense Grade 6 Mathematcis Page 1. Sequence Number Item Type: Multiple Choice (MC) or …


